Allereerst een tweetal formules, voordat begonnen kan worden met de berekening van de doorsnede van de lichtbundel. Dit zijn algemene formules uit de wiskunde, met een aanpassing van de symbolen aan de nevenstaande tekening.
In Nederland is het vaak de gewoonte om op grond van ervaring en inzicht te schatten hoe groot de bundel van een spot zal zijn op het moment dat hij de vloer of een object raakt. Dit wil nog wel eens tot verrassingen leiden, vooral als de ontwerper nog weinig ervaring heeft. Een bundel kan dan ineens veel te klein of juist te groot blijken te zijn, waardoor het ontwerp in zijn geheel in gevaar kan komen. Ter plekke moeten dan vaak snel beslissingen genomen worden, die niet altijd even gunstig uitpakken voor het eindresultaat. Vooral in de Verenigde Staten wordt gebruik gemaakt van formules om de grootte van een lichtbundel te bepalen. Hierdoor kan exact bepaald worden of een bepaalde spot wel de juiste bundel op de vloer of op het object kan maken, en kan dus van te voren besloten worden of een lichtontwerp al dan niet haalbaar is. Een nadeel van deze methode kan zijn dat de ontwerper zich te veel verliest in het rekenwerk, en weinig oog meer heeft voor het geheel van de voorstelling.
Beide methodes hebben zo hun voor en nadelen, een combinatie van beide is daarom aan te raden. Het maken van een lichtontwerp kan in eerste instantie het beste geschieden op grond van de eigen inzichten: zo heeft de ontwerper nog alle vrijheid van denken, zonder zich direct zorgen hoeven te maken over de exacte haalbaarheid. Nadat het ontwerp in principe is afgerond is het dan vervolgens zaak de spots, waarbij getwijfeld wordt over de haalbaarheid van de bundel, te controleren. Juist voor deze onderdelen van het ontwerp is het dan goed zich te richten op het rekenwerk: het ontwerp is dan eigenlijk al af, aansluitend op het bestaande toneelbeeld, het gaat dan alleen nog om de haalbaarheid van bepaalde details. Omdat een ontwerper op grond van zijn ervaring reeds zeker weet dat bepaalde effecten haalbaar zijn, hoeft hij niet alles door te rekenen. Maar om alle twijfel over de technische haalbaarheid uit te sluiten is het goed dat die onderdelen, waar hij niet zeker van is, nog eens goed doorgerekend worden. Formules zijn daarbij zeker niet zalig makend. Het feit dat een spot technisch in staat is een bepaalde bundel op de vloer te maken wil nog niet zeggen dat deze bundel ook goed in het geheel van het ontwerp zal passen. Het is daarbij vooral van belang om ook te letten op de lichtintensiteit. Een profielspot met een grote lenshoek, dus een spot die een grote lichtbundel kan maken, die gebruikt wordt om een uiterst kleine cirkel te maken, zal technisch in staat zijn deze bundel te maken. Door de grote lenshoek echter moet flink gebruik gemaakt worden van het diafragma. Doordat het diafragma veel van het licht tegen zal houden, zal de bundel qua grootte wel kloppen, maar qua lichtintensiteit heel donker over komen, veel donkerder dan allerlei andere spots. Als gevolg daarvan zullen percentages aangepast moeten worden, met als gevolg kleurverschillen in de bundels, of zal gebruik gemaakt moeten worden van zogenaamde "Neutral Density"-filters, met als mogelijk gevolg gebruik van twee filters in een spot. Dat laatste kan weer tot gevolg hebben, dat de filters sneller verkleuren of doorbranden, eventueel zelfs tijdens de voorstelling al.
Uiteraard zijn verkeerde inschattingen van een ontwerp tijdens de uitvoering nog grotendeels te corrigeren door gebruik te maken van allerlei handigheden. Maar ook hier geldt dat voorkomen beter is dan genezen.
Allereerst een tweetal formules, voordat begonnen kan worden met de berekening van de doorsnede van de lichtbundel. Dit zijn algemene formules uit de wiskunde, met een aanpassing van de symbolen aan de nevenstaande tekening.
In een aantal stappen zal nu verder de formule aangegeven worden die gebruikt kan worden voor de berekening van de grootte van d, dat is de doorsnede van de lichtbundel op de vloer, gemeten evenwijdig aan de richting waarin de spot schijnt. Daarbij wordt gebruik gemaakt van algemene wiskundige formules en de symbolen zoals deze in de bovenstaande afbeelding aangegeven zijn.tan A = l / h
Formule (1): Definitie van tangens
z² = h² + l²
Formule (2): Stelling van Pythagoras
Invullen van vergelijking (4) in vergelijking (3) levert het volgende op:tan(A - ½D) = (m - d) / h dus: m - d = h tan(A - ½D)
Formule (3)
tan(A + ½D) = m / h dus: m = h tan(A + ½D)
Formule (4)
Van deze nieuwe vergelijking (5) kan dan weer aan beide kanten de term h tan(A + ½D) afgetrokken worden, met als resultaat:h tan(A + ½D) - d = h tan(A - ½D)
Formule (5)
De term h kan dan aan de rechterzijde nog naar voren gehaald worden, zodat het uiteindelijk resultaat het volgende is:- d = h tan(A - ½D) - h tan(A + ½D) dus: d = h tan(A + ½D) - h tan(A - ½D)
Formule (6)
Met de bovenstaande formule (7) kan de zogenaamde lange as van de bundel berekend worden, daarnaast is ook de korte as van belang, de breedte van de lichtbundel, dwars op de richting waarin de bundel schijnt.d = h (tan(A + ½D) - tan(A - ½D))
Formule (7): Berekening van grootte d
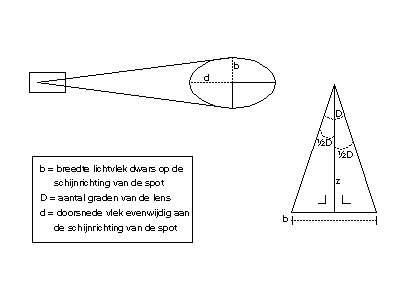
De symbolen en letters die gebruikt worden in de formules worden weer aangegeven in de nevenstaande tekening. Let er daarbij op, dat de letters voor grootheden die al eerder aan bod zijn gekomen, zoals bijvoorbeeld de afstand z of de lensopening D dezelfde zijn gebleven.
Uit de algemene formule (1) volgt, wanneer beide kanten met h vermenigvuldigd worden, de volgende vergelijking:
Kwadrateren van de bovenstaande vergelijking (8) levert het volgende op:l = h tan A
Formule (8)
Wordt de bovenstaande vergelijking (9) gecombineerd met de stelling van Pythagoras, die we terugvinden bij formule (2), dan kan de term l² bij de stelling van Pythagoras vervangen worden door de rechterhelft van vergelijking (9), met het volgende resultaat:l² = h² (tan A)²
Formule (9)
Bij de rechterhelft van de bovenstaande vergelijking (10) kan dan de term h² naar voren gehaald worden, zodat deze er als volgt uit komt te zien:z² = h² + h² (tan A)²
Formule (10)
Bij worteltrekken uit vergelijking (11) ontstaan twee mogelijke oplossingen, waarbij alleen de term met de positieve waarde van belang is voor het bepalen van de breedte van de bundel.z² = h² (1 + (tan A)²)
Formule (11)
Uit de afbeeldingen is verder op grond van de definitie van de tangens nog te bepalen dat:z = h (V(1 + (tan A)²))
Formule (12)
Waarbij (V() staat voor "de wortel uit"
waaruit weer volgt dat:tan(½D) = ½ b / z dus: tan(½D) = b / 2z
Formule (13)
Wanneer de vergelijking (12) ingevuld wordt bij de zojuist gevonden vergelijking (14), wordt het volgende resultaat verkregen, dat gebruikt kan worden voor de bepaling van de waarde b , de breedte van een lichtbundel, gemeten op de dwarsrichting van de richting waarin de spot schijnt:b = 2 z tan(½D)
Formule (14)
Met behulp van de formules (7) en (15) kunnen de waarden die van direct belang zijn bij het bepalen van de grootte van een lichtbundel berekend worden. De twee assen die hiermee berekend zijn bepalen in principe de gehele bundel, al moet gezegd worden dat deze benadering niet exact is. Maar binnen de marges zijn dit hanteerbare formules die voldoende resultaat opleveren.b = 2 h tan(½D) (V(1 + (tan A)²)
Formule (15): Bepaling van de breedte van een bundel
Ter controle van de formules kan nog gekeken worden naar een bijzonder geval, namelijk wanneer een spot top hangt, dus wanneer geldt dat de invalshoek A= 0 graden. Bij een dergelijke bundel wordt namelijk een cirkel verkregen, en voor een cirkel geldt dat de beide assen van de bundel even groot moeten zijn. Of dit ook zo is binnen de formules kan bekeken worden door in de formules (7) en (15) voor A de waarde 0 in te vullen. De waarden voor b en d moeten dan gelijk zijn.
Allereerst voor formule (7):
Uit de definitie van de tangens volgt dat:d = h (tan (0 + ½D) - tan (0 - ½D)) dus: d = h (tan (½D) - tan (-½D))
Formule (16)
dus vergelijking (16) kan ook als volgt geschreven worden:tan -D = - tan D
Formule (17)
Vervolgens kan de waarde D = 0 ingevuld worden in formule (15), waarbij het uiteindelijke resultaat vergeleken zal moeten worden met het resultaat in vergelijking (18). Uit die vergelijking zou dan uiteindelijk moeten volgen dat b = d .d = h (tan (½D) + tan (½D)) dus: d = 2 h tan (½D)
Formule (18)
Wanneer de vergelijkingen (18) en (19) met elkaar vergeleken worden volgt daar inderdaad uit dat de waarden voor b en d gelijk zijn.b = 2 h tan(½D) (V(1 + (tan 0)²) dus: b = 2 h tan (½D) (V(1 + 0) dus: b = 2 h tan (½D)
Formule (19)
In principe zijn van alle vergelijkingen die hier naar voren gekomen zijn alleen formule (7) en (15) van belang bij het berekenen van de grootte van een lichtbundel. Voor de overzichtelijkheid worden ze hieronder nog een keer gegeven.
d = h (tan(A + ½D) - tan(A - ½D))
Berekening van grootte d
Waarbij:d = Doorsnede van de lichtbundel evenwijdig aan de richting waarin de spot schijnt;
h = Hoogte van de spot;
A = Hellingshoek van de spot;
D = Aantal graden van de lens, de zogenaamde lenshoek.
b = 2 h tan(½D) (V(1 + (tan A)²)
Bepaling van de breedte b van een bundel
Waarbij:b = Breedte van de lichtbundel dwars op de richting waarin de spot schijnt;
h = Hoogte van de spot;
D = Aantal graden van de lens, de zogenaamde lenshoek of lensopening;
A = Hellingshoek van de spot.
Terug naar Inhoudsopgave